从自编码器到变分自编码器

自编码器

特点：

• 无监督神经网络。
• 发现数据内在隐藏结构和潜在变量。
• 将输入复制到输出，网络中间设置的架构约束迫使模型学习一种有意义的压缩表示。
• 损失函数用于衡量原始输入与重构输出之间的差异。

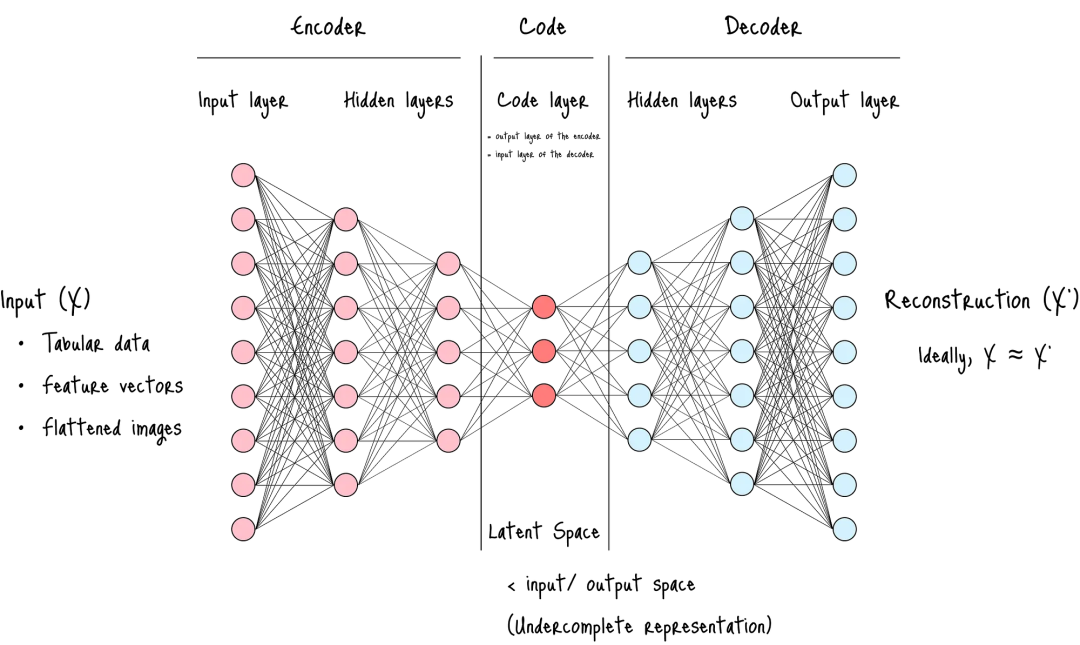
关键结构：

• 编码器（Encoder）: 本质上扮演着一个特征提取器的角色，将原始数据转化为一个更紧凑、信息更密集的表示。
• 潜空间（Latent Space）: 压缩程度最高的一层，是整个架构最关键的部分，迫使网络筛选并保留对重构至关重要的核心信息，而丢弃冗余和噪声。
• 解码器（Decoder）: 其结构通常与编码器镜像对称。它接收来自瓶颈层的压缩表示，并尝试将其“解压”，以重构出原始的高维输入数据。

关键超参：

• 编码大小（Code Size）: 即潜空间的维度。这是最关键的超参数，它直接控制了数据的压缩程度，并扮演着强大的正则化角色。较小的潜空间会降低过拟合的风险，但可能丢失重要信息；反之，较大的瓶颈层则可能导致模型学习到恒等函数，失去压缩的意义。
• 层数（Number of Layers）: 编码器和解码器的深度。更多的层数使模型能够学习更复杂的非线性关系，但同时也增加了计算成本和过拟合的风险。
• 每层节点数（Nodes per Layer）: 各层的宽度，通常构成一个对称的漏斗状结构。
• 重构损失函数（Reconstruction Loss）: 损失函数的选择至关重要，它取决于输入数据的性质。对于连续数据，通常使用均方误差（Mean Squared Error, MSE）；对于二元数据，则可使用二元交叉熵（Binary Cross-Entropy）。

自编码器的架构本身就体现了信息保留与模型泛化之间的一种权衡，潜空间的编码大小是这种权衡的直接体现。

自编码器：

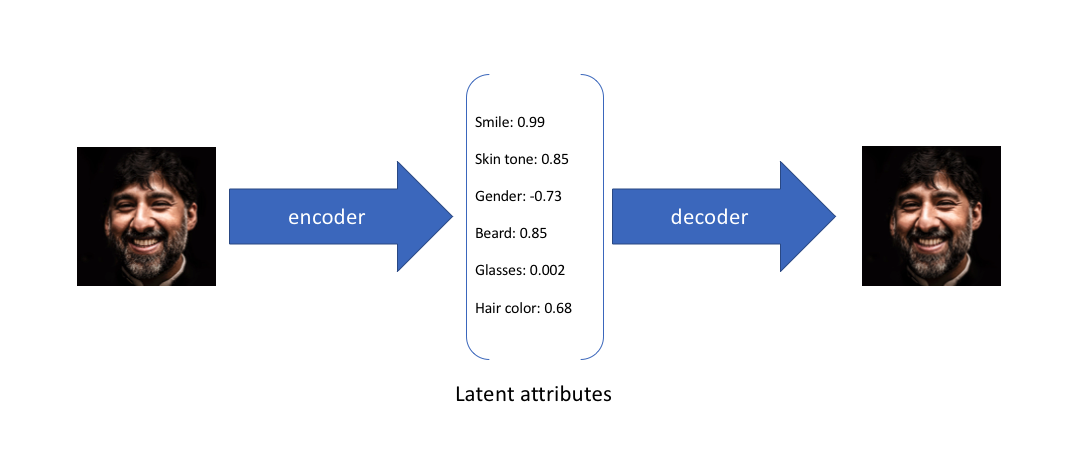
由于自编码器仅关注隐层编码的重建能力，其隐层空间分布往往是无规律和不均匀的，在连续的隐层空间随机采样或者插值得到一组编码通常会产生无意义和不可解释的生成结果。

变分自编码器

为了构建一个有规律的隐层空间，使得我们可以在不同潜在属性上随机地采样和平滑地插值，最后通过解码器生成有意义的图像，研究者们在2014年提出了变分自编码器。

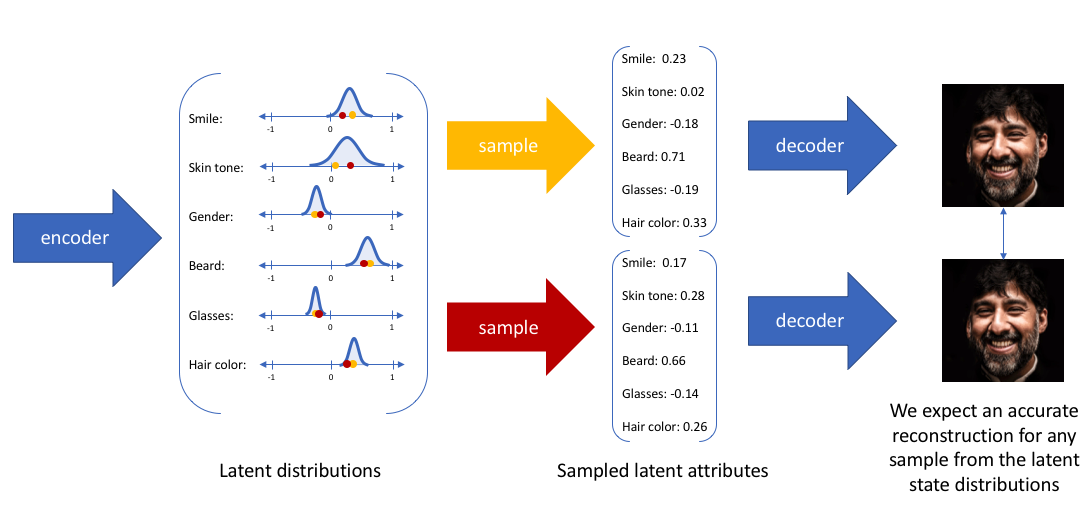
变分自编码器不再将输入映射成隐层空间中的一个固定编码，而是转换成对隐层空间的概率分布估计。

变分自编码器：

如何估计$p(x)$

首先我们现在的目标是要求出一个概率分布。即我们随机生成的这样一个图片X，其取值为a的概率为 $p(a)$ （即 $P(X=a)=p(a)$ ），目的就是求出这个满足我们要求的分布。只要我们能求出合适的分布，我们就可以通过对这个分布进行采样得到我们期望的图片了。

估计分布有两种方法：

• 极大似然估计（往往p(x)未知，且参数空间巨大）
• 隐变量估计

隐变量模型顾名思义，就是引入隐变量，期望从简单的分布 $p(z)$ 出发，用积分公式来间接求出复杂的 $p(x)$。隐变量模型背后的关键思想是：任何一个简单的概率分布经过一个足够复杂的函数后可以映射到任意概率分布：

$p(x)=\int_{}^{}p(x|z)p(z)dz$。

接下来要解决的就是 $p(x|z)$ 和 $p(z)$。

$p(z)$ 可以很简单，$z$自由度低，例如是普通的多元高斯分布。

$p(x|z)$ 可以是个确定性的过程 $p_\theta(x|z)$，即 $x=f(z)$, $f$ 用神经网络来表示。（解码过程）

从 $p(z)$ 到 $p(x)$ 的过程分为：

• 1.假设想得到 $p(x = x^’)$ 的概率，那么就先研究 $f$ 找到所有 $z$，使得 $x^’ = f(z)$。

• 2.假设 $z$ 的解集合为｛$z_1$, $z_2$, … $z_m$｝ ，则把这些 $z$ 出现的概率全部加起来就是 $x^’$ 出现的概率，即可以得到 $p(x=x^’) = \sum_{i=1}^{m}p(z=z_i)$。

但求 $z$ 的解集合是很难的。所以虽然 $p(z)$ 很简单，$f$ 是个确定过程，但由于 $f$ 不一定可逆，$p(x)$ 仍然很难直接算出表达式。

所以是用蒙特卡洛方法得到 $p(x)$ 的近似解。原本的积分可以表示成期望的形式 $\int_{}^{}p_\theta(x|z)s(z)dz = E_{z-s(z)}[p\theta(x|z)]$ ，我们可以通过采样估计期望来估计积分。

为提高采样效率。这里的 $K$ 可能需要非常大才能得到对应满意的结果，也就是生成一个 $x^’$ 需要很多次 $z$ 的采样。因此一种思路是提高$z$ 的采样效率，最好采样一次就能完成任务。这就是 VAE 的研究方向。

VAE

如何提高 $z$ 的采样效率呢？一种思路是用 $p(z|x)$ 来估计 $p(z)$，原因是有了 $x$ 的信息，$z$ 怎么着都应该变得确定一点吧。这里研究的变量是 $z$，因此 $p(z)$ 是先验分布，$p(z|x)$ 是后验分布。但即便如此，无中生有出 $p(z|x)$ 会陷入鸡生蛋和蛋生鸡的窘境，我们需要一个具体可优化模型来逼近 $p(z|x)$，于是引入新的概率分布 $q_\theta(z|x)$。思路逐渐清晰了。

关于VAE的数学部分，详细参考： VAE章节。

设计初衷

过概率模型对数据的生成过程进行建模，使得生成的潜在表示服从某种先验分布（通常是高斯分布），从而使模型具备更强的生成能力。VAE的设计动机可以概括为以下几点：

• 生成新数据的能力：自动编码器只能进行重构而不是生成新的数据，而VAE通过在潜在空间中引入概率分布，使得从潜在空间中采样可以生成多样化且有效的数据样本。 潜在空间的结构化：VAE通过引入先验分布（如标准正态分布），让潜在空间具备更好的结构，模型能够学习到数据的真实分布。这样在潜在空间中采样时，可以生成具有多样性的、与原始数据相似的新样本。
• 解决过拟合问题：传统的自动编码器在重建输入数据时可能会过拟合，导致潜在空间的分布非常不连续，VAE通过变分推断的方法，在训练过程中加入KL散度正则项，鼓励潜在表示接近先验分布，从而防止过拟合。
• 利用概率图模型的思想：VAE结合了概率图模型和深度学习的优点，将数据生成过程建模为一个隐变量模型，并通过变分推断的方式进行训练。
• 进行隐式的数据增强：单从数学表示来看，VAE求得隐变量的过程 Z = μ + ε × σ 相较于AE，实际上就是在AE所求的 \text{z} （对应VAE中的 \mu ）上新加了一个方差为 \sigma^2 的高斯噪声，故可以认为是在对每次输入的数据在隐藏空间内做一个基于加噪的数据增强，这种设计不仅能防止过拟合，还提升了模型的泛化能力和生成质量。（可以理解为：VAE的隐变量采样过程与经典的数据增强策略在概念上类似，只不过它作用于潜在空间而非直接的输入空间。）

训练过程：向encoder输入图像 -> encoder生成潜在分布 -> 重参数化采样 -> decoder重建图像 -> 最小化重构损失和KL散度。

推理过程：直接从潜在空间（标准正态分布）采样潜在变量 -> 解码器生成新图像。

参考：

生成式模型汇总。